Thermo-mechanical NTFA - Generate input files
Felix Fritzen fritzen@simtech.uni-stuttgart.de, Julius Herb julius.herb@mib.uni-stuttgart.de, Shadi Sharba shadi.sharba@isc.fraunhofer.de
University of Stuttgart, Institute of Applied Mechanics, Chair for Data Analytics in Engineering
Funding acknowledgment The IGF-Project no.: 21.079 N / DVS-No.: 06.3341 of the “Forschungsvereinigung Schweißen und verwandte Verfahren e.V.” of the German Welding Society (DVS), Aachener Str. 172, 40223 Düsseldorf, Germany, was funded by the Federal Ministry for Economic Affairs and Climate Action (BMWK) via the German Federation of Industrial Research Associations (AiF) in accordance with the policy to support the Industrial Collective Research (IGF) on the orders of the German Bundestag.
Felix Fritzen is funded by the German Research Foundation (DFG) – 390740016 (EXC-2075); 406068690 (FR2702/8-1); 517847245 (FR2702/10-1).
Imports
[1]:
import os
import sys
from itertools import count
import h5py
import matplotlib.pyplot as plt
import numpy as np
data_path = "../data"
Load H5 file with validation simulations
While the NTFA is trained based on snapshots at 10 temperature points, this data set contains snapshots at 100 temperature points.
[2]:
file_name = os.path.join(
data_path, "ntfa_raw", "rve_thermoplastic_6loadings_10samples.h5"
)
group_name = "/ms_9p/dset0_sim"
suffix = "_fix16_N24_100s"
prefix = os.path.join(data_path, "loadcases")
N_modes = 24
# open the file an get the keys --> extract temperatures!
F = h5py.File(file_name, "r")
keylist = F[group_name].keys()
temp_list = []
temp_str_list = []
for k in keylist:
if k[:13] == "hom_response_":
temp_list.append(float(k[13:20]))
temp_str_list.append(k[13:20])
# get loadings:
loadcases = np.array(F[group_name + "/loadcases_" + temp_str_list[0]])[-1, :, :].T
# find proportional loadings, figure direction and amplitude:
fans_S = []
fans_S0 = []
fans_S1 = []
for t_str in temp_str_list:
fans_S.append(
np.transpose(np.array(F[group_name + "/hom_response_" + t_str]), axes=(2, 0, 1))
)
fans_S0.append(
np.transpose(
np.array(F[group_name + "/hom_response0_" + t_str]), axes=(2, 0, 1)
)
)
fans_S1.append(
np.transpose(
np.array(F[group_name + "/hom_response1_" + t_str]), axes=(2, 0, 1)
)
)
F.close()
Generate input files (*.inp) for FE simulation on macroscale
The thermo-mechanical NTFA is used as effective material model in the FE simulation on macroscale.
[3]:
ntfa_S = []
ntfa_S0 = []
ntfa_S1 = []
modefn = os.path.join(data_path, "ntfa", "ms9p_fix_ntfa16_B1-6_10s_N24.h5")
orig_stdout = sys.stdout
amplitudes = np.ones(loadcases.shape[0])
for n, d, amp in zip(count(), loadcases, amplitudes):
for T, T_str in zip(temp_list, temp_str_list):
f = open(os.path.join(prefix, f"loadcase{n + 1}_T{T_str}{suffix}.inp"), "w")
sys.stdout = f
print(f'output="loadcase{n + 1}_T{T_str}{suffix}.h5";')
print(f'modes="{modefn}";')
print(f"epsilon=[{d[0]}, {d[1]}, {d[2]}, {d[3]}, {d[4]}, {d[5]}];")
print(f"amplitude={amp};")
print("totaltime=1;")
print("deltat=0.1;")
print(f"tstart={T};")
print(f"tend={T};")
print("hardeningmodulus=500000.0;")
# print("hardeningmodulus=20000000.0;")
print("elastic=false;")
print("relaxthermo=false;")
print("linhardening=true;")
f.close()
sys.stdout = orig_stdout
Post-process results of FE simulation on macroscale
[4]:
ntfa_eps = np.zeros(
(len(temp_list), fans_S[0].shape[0], fans_S[0].shape[1], fans_S[0].shape[2])
)
ntfa_S = np.zeros(
(len(temp_list), fans_S[0].shape[0], fans_S[0].shape[1], fans_S[0].shape[2])
)
ntfa_S0 = np.zeros(
(len(temp_list), fans_S[0].shape[0], fans_S[0].shape[1], fans_S[0].shape[2])
)
ntfa_S1 = np.zeros(
(len(temp_list), fans_S[0].shape[0], fans_S[0].shape[1], fans_S[0].shape[2])
)
ntfa_q = np.zeros((len(temp_list), fans_S[0].shape[0], fans_S[0].shape[1]))
ntfa_xi = np.zeros((len(temp_list), fans_S[0].shape[0], fans_S[0].shape[1], N_modes))
ct = 0
print(ntfa_S1.shape)
for i_T, (T, T_str) in enumerate(zip(temp_list, temp_str_list)):
for n, d, amp in zip(count(), loadcases, amplitudes):
ntfa_fname = os.path.join(prefix, f"loadcase{n + 1}_T{T_str}{suffix}.h5")
# print(ntfa_fname)
F_ntfa = h5py.File(ntfa_fname, "r")
# get references values:
ntfa_eps[i_T, n, :, :] = np.array(F_ntfa["/eps"])
ntfa_S[i_T, n, :, :] = np.array(F_ntfa["/sig"])
ntfa_S0[i_T, n, :, :] = np.array(F_ntfa["/sig0"])
ntfa_S1[i_T, n, :, :] = np.array(F_ntfa["/sig1"])
ntfa_q[i_T, n, :] = np.array(F_ntfa["/sdv"][:, 0])
ntfa_xi[i_T, n, :] = np.array(F_ntfa["/sdv"][:, 1 : (1 + N_modes)])
F_ntfa.close()
print(ntfa_S1[0][5])
print(ntfa_S1[9][5])
(10, 6, 11, 6)
[[-3.94059291e+04 -3.94059291e+04 -3.94059291e+04 2.14816003e+01
2.14816003e+01 2.14816003e+01]
[ 8.65907872e+04 8.65907872e+04 8.65907872e+04 2.59256527e+02
2.59256527e+02 2.59256527e+02]
[ 2.12587503e+05 2.12587503e+05 2.12587503e+05 4.97031453e+02
4.97031453e+02 4.97031453e+02]
[ 3.38584220e+05 3.38584220e+05 3.38584220e+05 7.34806380e+02
7.34806380e+02 7.34806380e+02]
[ 4.64580936e+05 4.64580936e+05 4.64580936e+05 9.72581306e+02
9.72581306e+02 9.72581306e+02]
[ 5.90577652e+05 5.90577652e+05 5.90577652e+05 1.21035623e+03
1.21035623e+03 1.21035623e+03]
[ 7.16574368e+05 7.16574368e+05 7.16574368e+05 1.44813116e+03
1.44813116e+03 1.44813116e+03]
[ 8.42571085e+05 8.42571085e+05 8.42571085e+05 1.68590609e+03
1.68590609e+03 1.68590609e+03]
[ 9.68567801e+05 9.68567801e+05 9.68567801e+05 1.92368101e+03
1.92368101e+03 1.92368101e+03]
[ 1.09456452e+06 1.09456452e+06 1.09456452e+06 2.16145594e+03
2.16145594e+03 2.16145594e+03]
[ 1.22056123e+06 1.22056123e+06 1.22056123e+06 2.39923086e+03
2.39923086e+03 2.39923086e+03]]
[[-4.13855117e+05 -4.13855026e+05 -4.13803441e+05 -1.02069696e+03
-1.02250133e+03 -1.02262612e+03]
[-4.04227656e+05 -4.04227565e+05 -4.04175980e+05 -9.13226517e+02
-9.15030890e+02 -9.15155681e+02]
[-3.94600195e+05 -3.94600104e+05 -3.94548519e+05 -8.05756074e+02
-8.07560447e+02 -8.07685238e+02]
[-3.84972734e+05 -3.84972644e+05 -3.84921058e+05 -6.98285631e+02
-7.00090004e+02 -7.00214796e+02]
[-3.75345273e+05 -3.75345183e+05 -3.75293597e+05 -5.90815189e+02
-5.92619561e+02 -5.92744353e+02]
[-3.65869629e+05 -3.65869726e+05 -3.65822921e+05 -4.82471805e+02
-4.84376885e+02 -4.84509212e+02]
[-3.59278427e+05 -3.59290446e+05 -3.59303289e+05 -3.73168736e+02
-3.76218567e+02 -3.76405027e+02]
[-3.52716030e+05 -3.52744407e+05 -3.52792614e+05 -2.76002715e+02
-2.79615262e+02 -2.79769692e+02]
[-3.46175548e+05 -3.46222255e+05 -3.46289018e+05 -1.88514783e+02
-1.92293079e+02 -1.92342595e+02]
[-3.39651955e+05 -3.39717389e+05 -3.39791235e+05 -1.08834296e+02
-1.12512000e+02 -1.12398267e+02]
[-3.33141519e+05 -3.33225105e+05 -3.33298360e+05 -3.55216659e+01
-3.89244428e+01 -3.86031012e+01]]
Compute error of stresses
Overall stress: \(S\), Stress in phase 0: \(S_0\), Stress in phase 1: \(S_1\)
[5]:
err = np.linalg.norm(fans_S - ntfa_S, axis=(2, 3)) / np.linalg.norm(fans_S, axis=(2, 3))
err0 = np.linalg.norm(fans_S0 - ntfa_S0, axis=(2, 3)) / np.linalg.norm(
fans_S, axis=(2, 3)
)
err1 = np.linalg.norm(fans_S1 - ntfa_S1, axis=(2, 3)) / np.linalg.norm(
fans_S, axis=(2, 3)
)
Plot stresses (NTFA vs. reference)
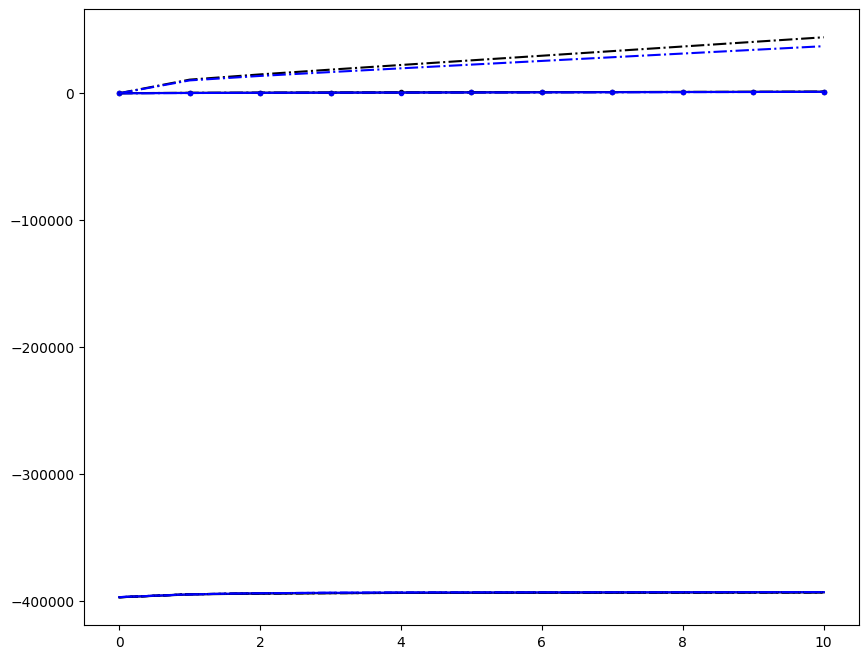
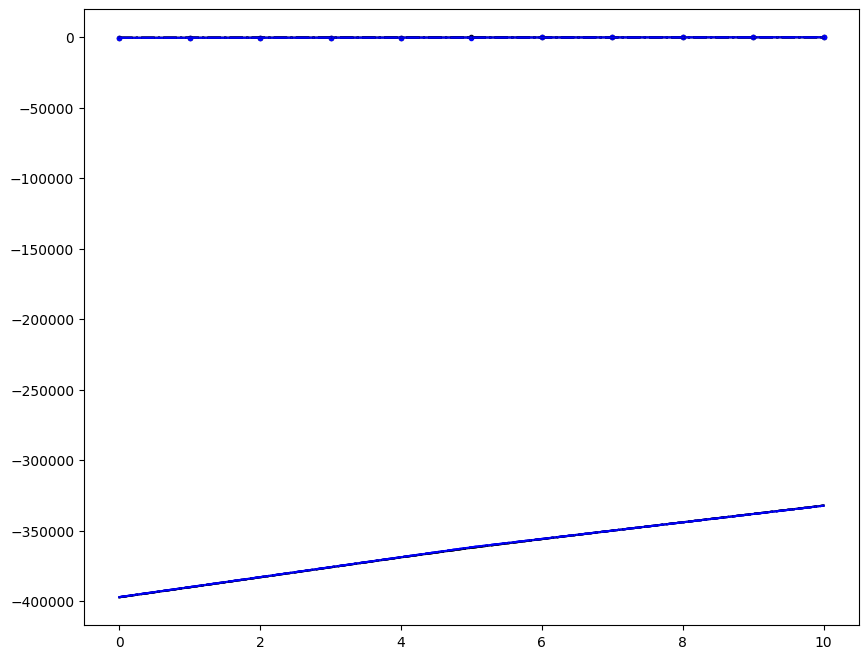
Incremenent \(i_T = 9\); all loading directions \(1 \leq n \leq 6\)
[6]:
i_T = 9
for n in range(6):
fig, ax1 = plt.subplots(1, 1, figsize=(10, 8))
# fig, ax2 = plt.subplots(1,1,figsize=(10,8))
# fig, ax3 = plt.subplots(1,1,figsize=(10,8))
# for i, dp in zip( (0,), ('--',) ):
for i, dp in enumerate(("-", "--", "-.", "-..", "-", "-.")):
ax1.plot(fans_S[i_T][n][:, i], dp, color="black")
# ax1.plot( (fans_S[i_T][n][:,i]-ntfa_S[i_T][n][:,i])/1e3, dp, color='black' )
# print(fans_S[i_T][n][:,i]-ntfa_S[i_T][n][:,i])
ax1.plot(ntfa_S[i_T][n][:, i], dp, color="blue")
# ax2.plot( fans_S0[i_T][n][:,i], dp, color='black' )
# ax2.plot( ntfa_S0[i_T][n][:,i], dp, color='blue' )
# ax1.plot( fans_S1[i_T][n][:,i], dp, color='black' )
# ax1.plot( ntfa_S1[i_T][n][:,i], dp, color='blue' )
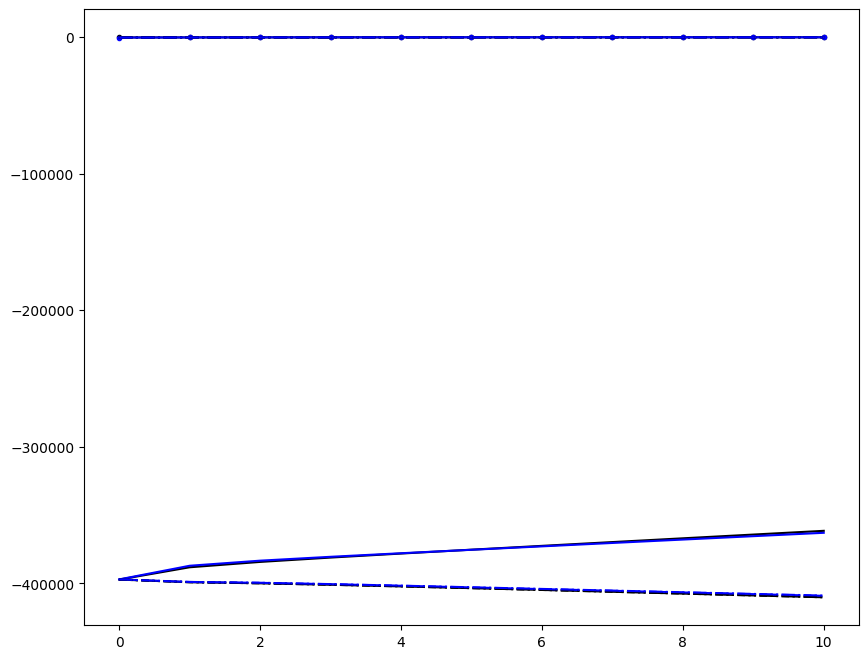
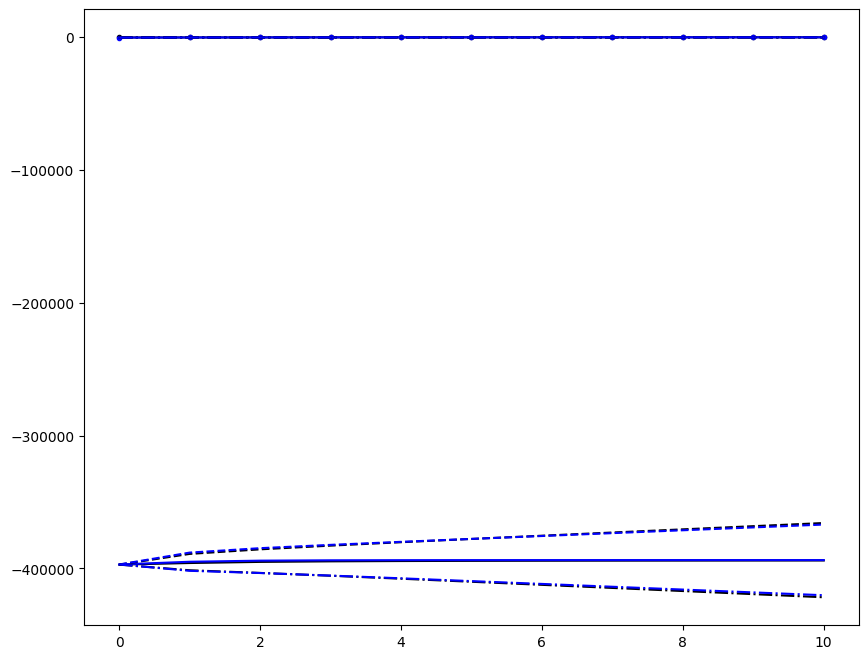
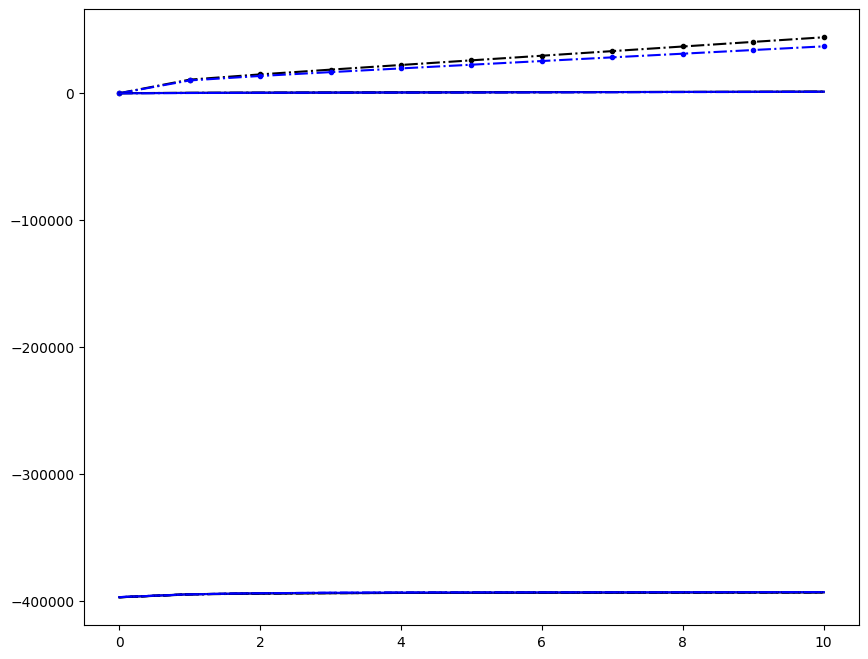
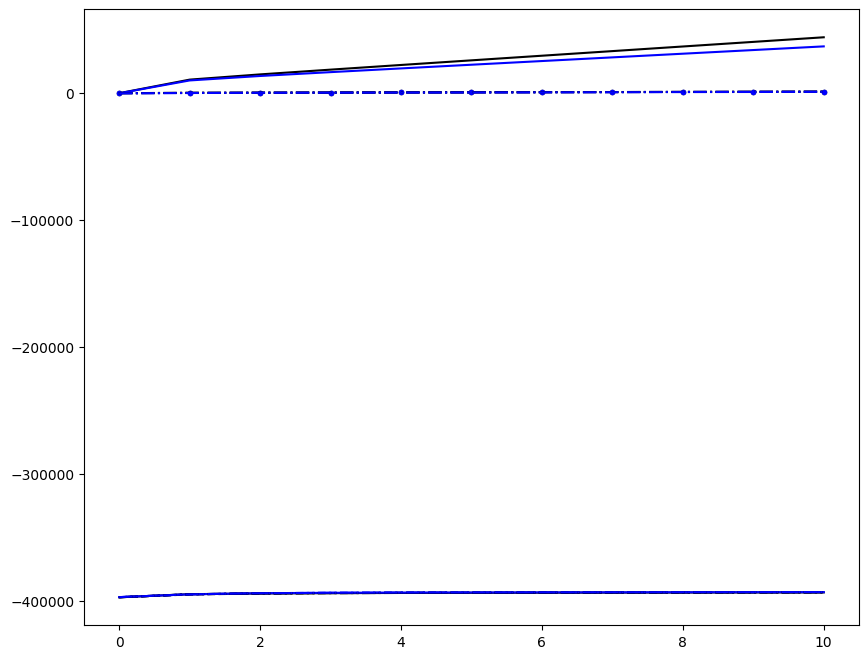
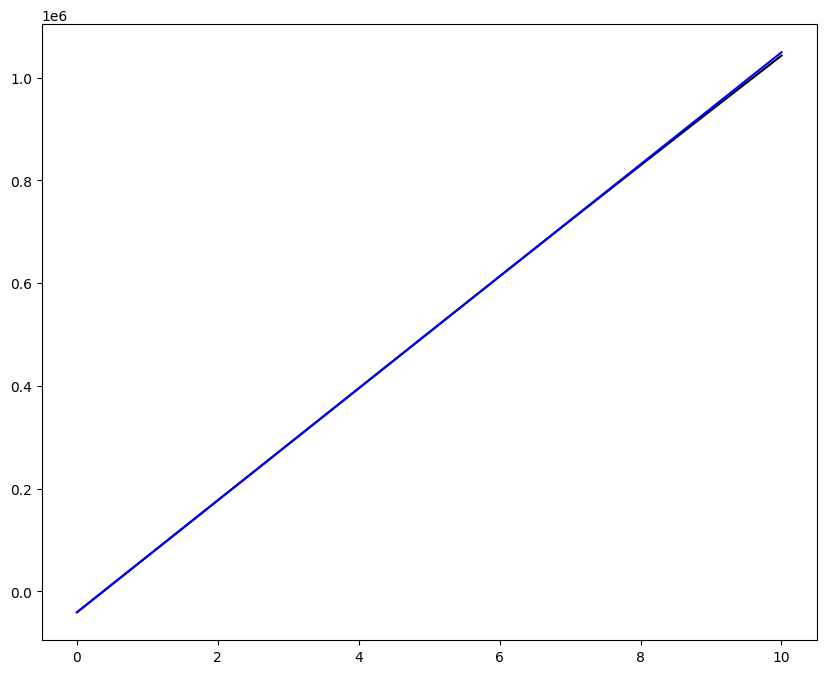
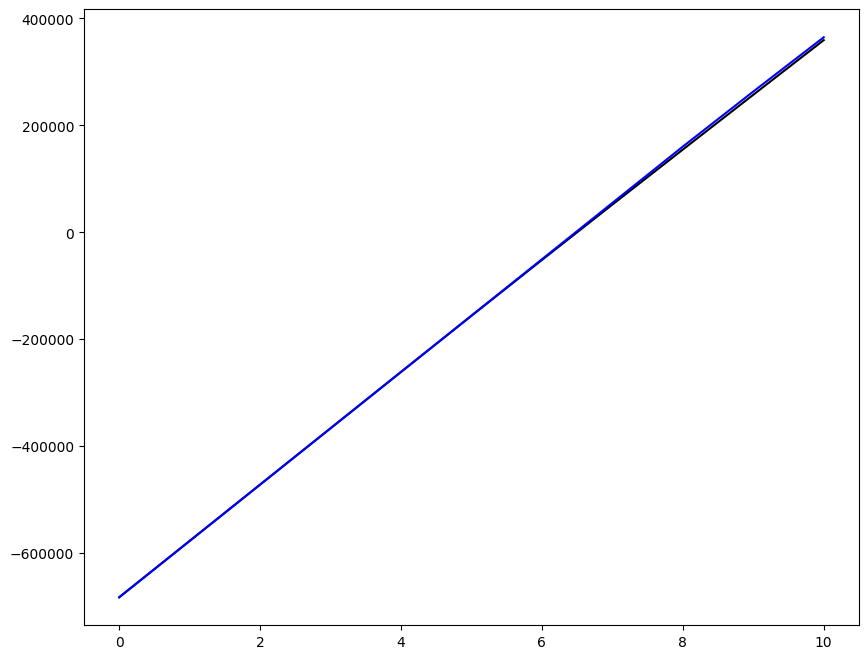
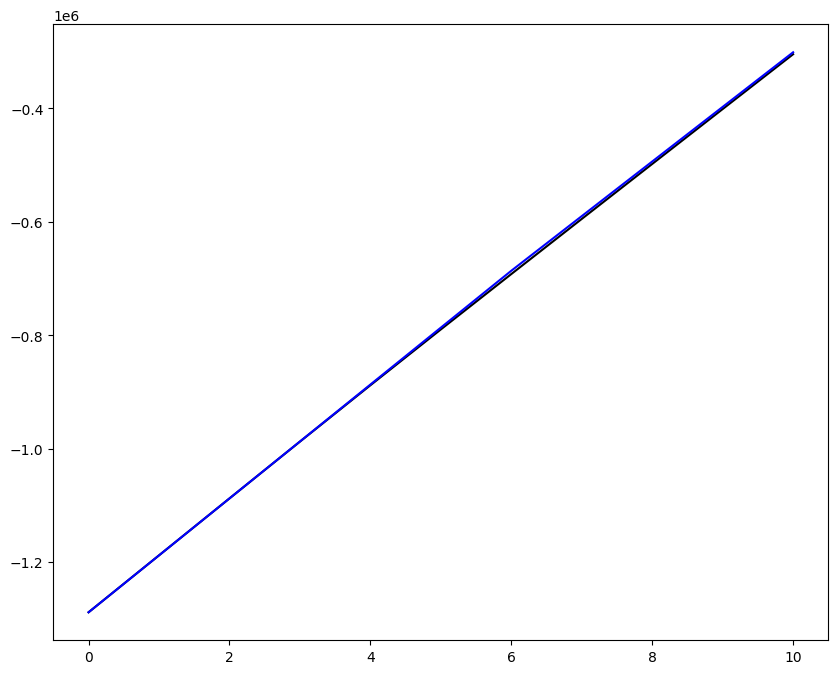
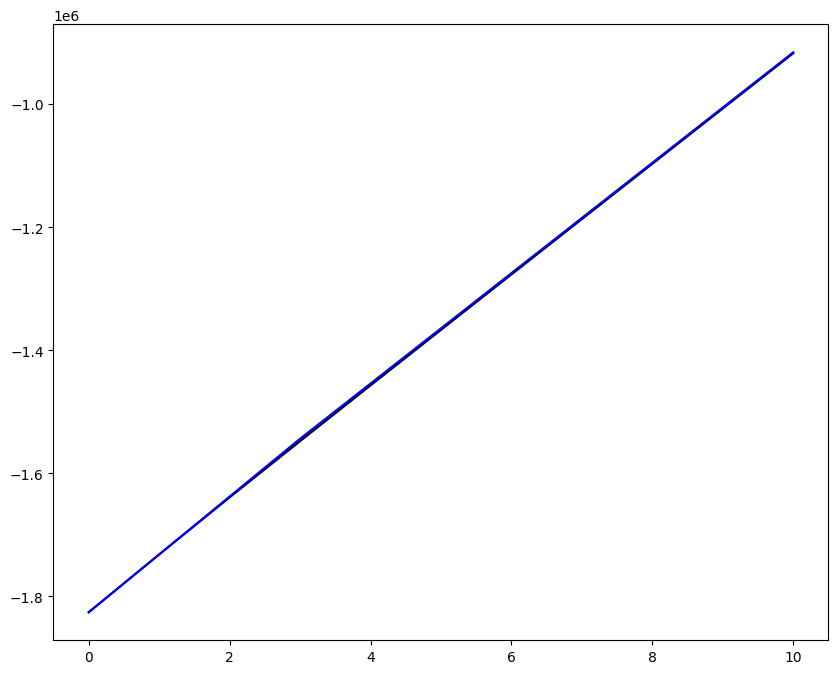
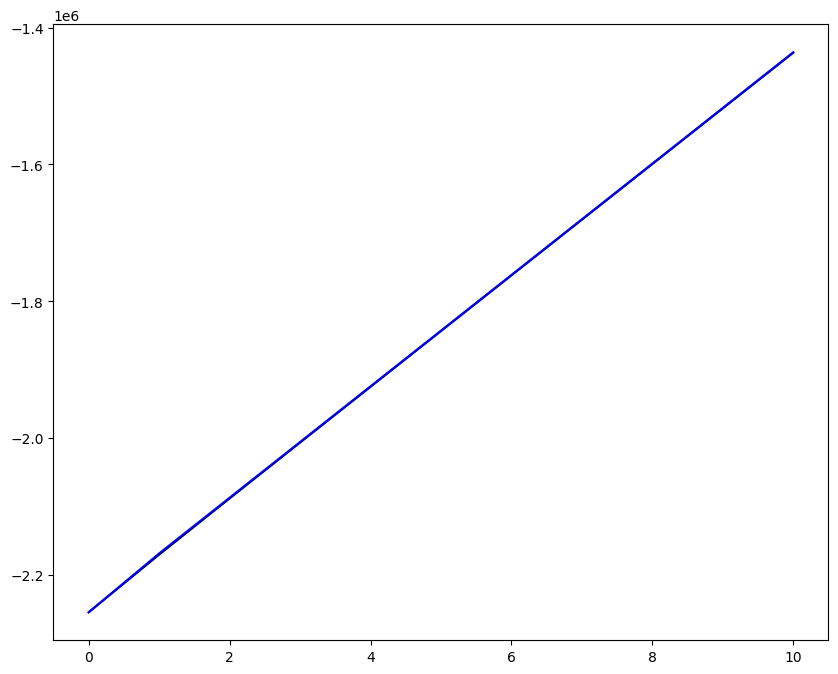
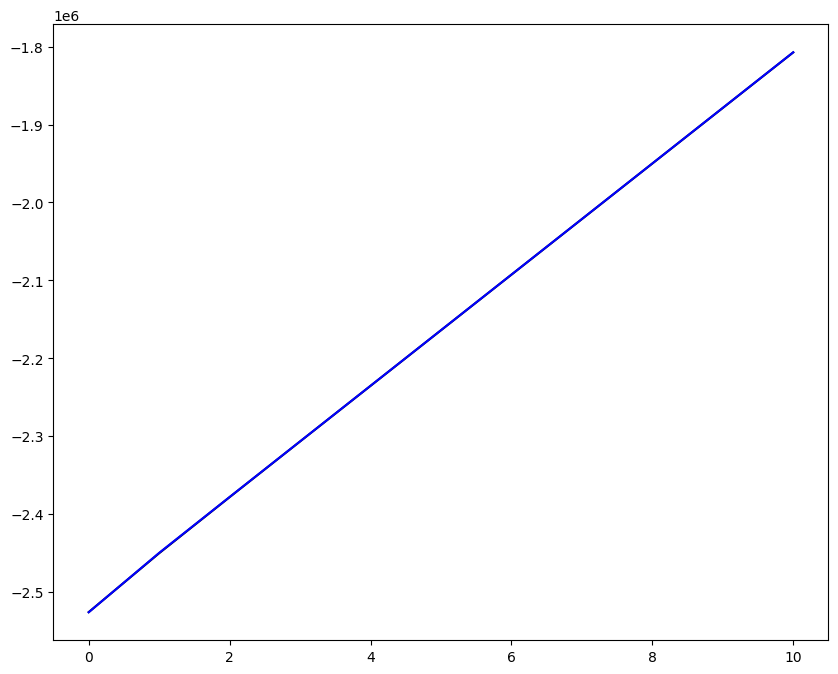
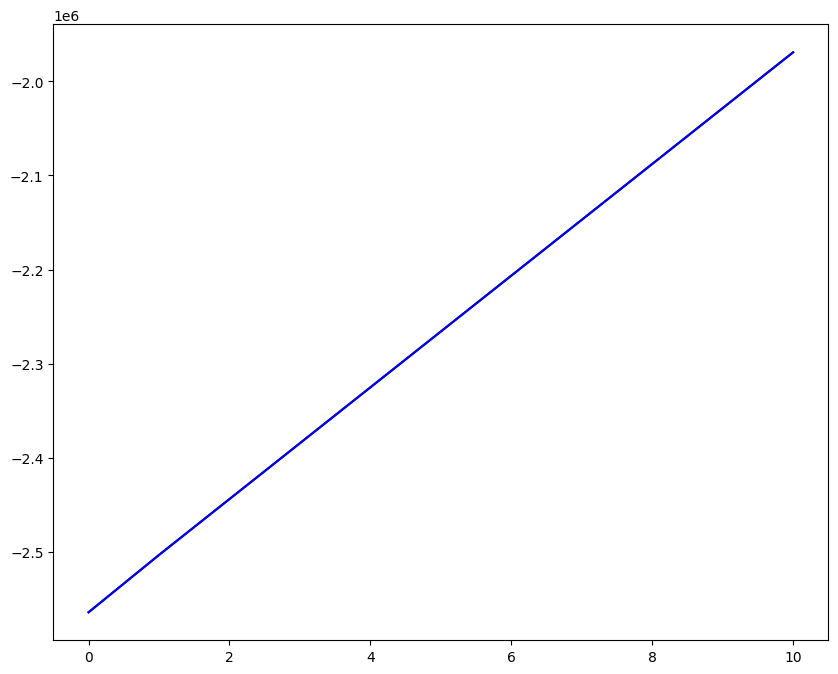
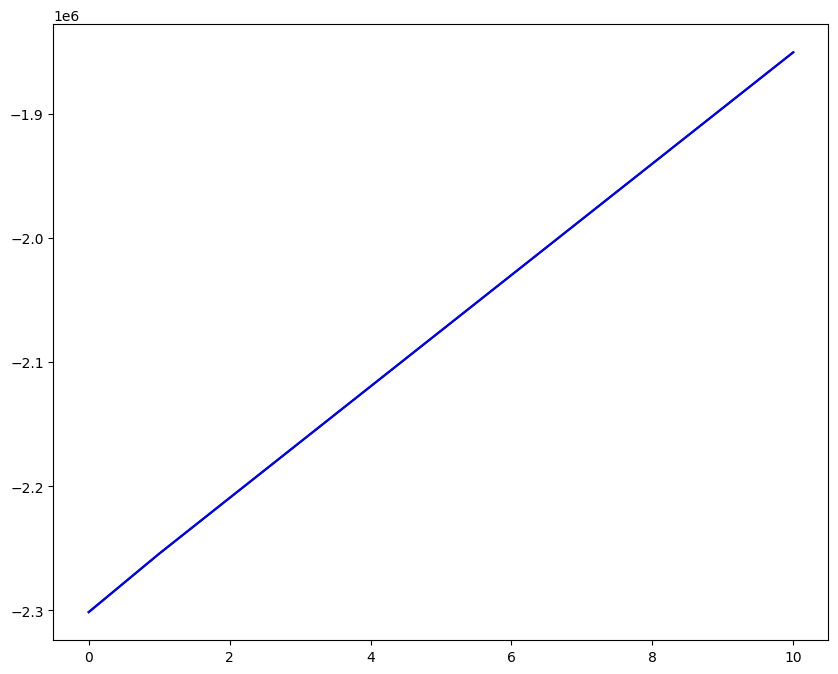
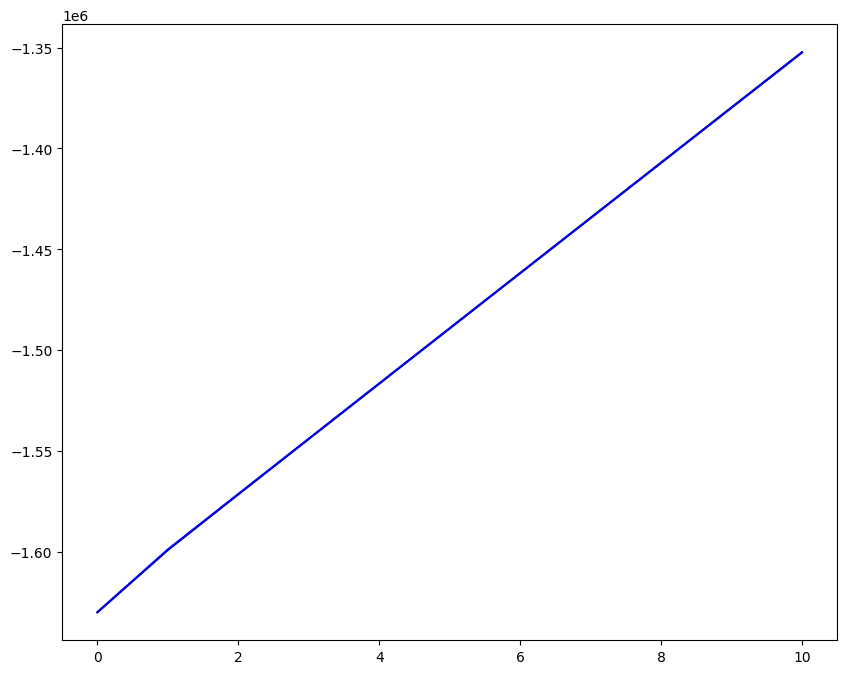
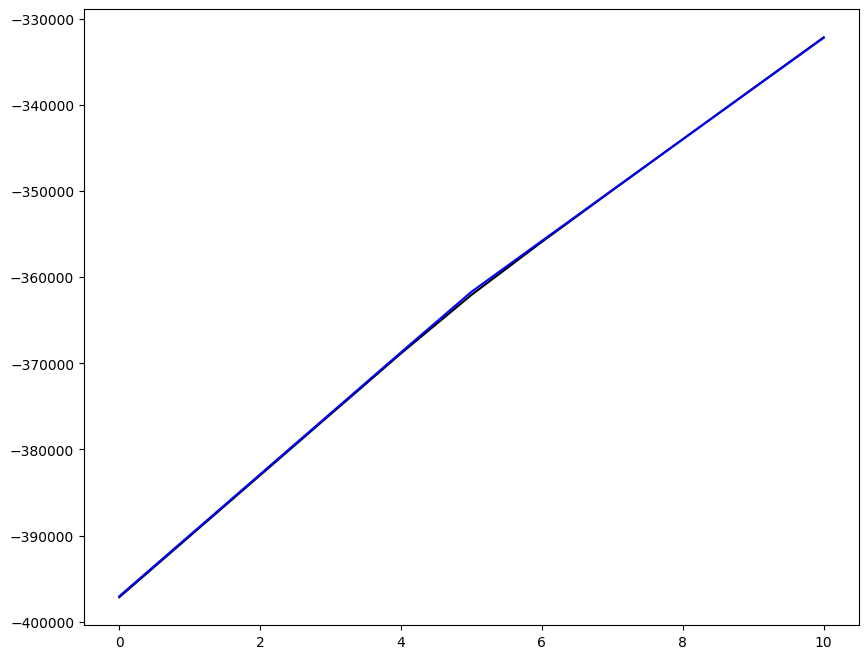
Loading direction \(n = 5\); all increments \(0 \leq i_T \leq 9\)
[7]:
n = 5
for i_T in range(10):
fig, ax1 = plt.subplots(1, 1, figsize=(10, 8))
# fig, ax2 = plt.subplots(1,1,figsize=(10,8))
# fig, ax3 = plt.subplots(1,1,figsize=(10,8))
for i, dp in zip((3,), ("-",)):
# for i, dp in enumerate(("-", "--", "-.", "-..", "-","-.")):
ax1.plot(fans_S[i_T][n][:, 0], dp, color="black")
# ax1.plot( (fans_S[i_T][n][:,i]-ntfa_S[i_T][n][:,i])/1e3, dp, color='black' )
# print(fans_S[i_T][n][:,i]-ntfa_S[i_T][n][:,i])
ax1.plot(ntfa_S[i_T][n][:, 0], dp, color="blue")
# ax1.plot( ntfa_q[i_T][n][:], '-', color='red', lw=2)
# ax2.plot( fans_S0[i_T][n][:,i], dp, color='black' )
# ax2.plot( ntfa_S0[i_T][n][:,i], dp, color='blue' )
# ax1.plot( fans_S1[i_T][n][:,i], dp, color='black' )
# ax1.plot( ntfa_S1[i_T][n][:,i], dp, color='blue' )
# ## Plot relative error (NTFA vs. reference)
#
# ### Overall stress
[8]:
fig, axx = plt.subplots(1, 2, figsize=(15, 7))
ct = 0
for i_T, T in zip((0, 9), (300.0, 1300.0)):
ax = axx[ct]
ct += 1
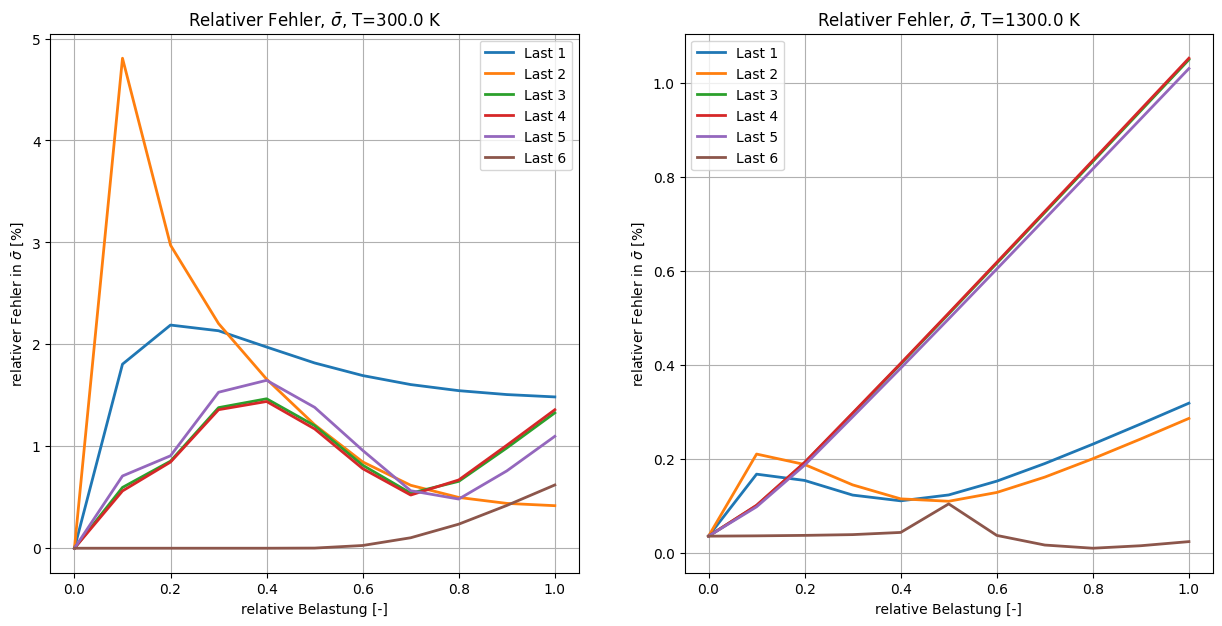
ax.set_title(r"Relativer Fehler, $\bar{\sigma}$, T=%.1f K" % T)
x = np.linspace(0, 1, 11)
ax.set_xlabel("relative Belastung [-]")
ax.set_ylabel(r"relativer Fehler in $\bar{\sigma}$ [%]")
for n in range(6):
myerr = (
np.linalg.norm(fans_S[i_T][n][:, :] - ntfa_S[i_T][n][:, :], axis=1)
* 100.0
/ np.linalg.norm(fans_S[i_T][n][:, :], axis=1)
)
ax.plot(x, myerr, lw=2, label=f"Last {n + 1}")
# print(np.max(myerr))
ax.legend()
ax.grid()
# fig.savefig( f'rel_error_ms9p_T{T:.0f}.pdf', format='pdf', pad_inches=0.0)
plt.savefig("rel_err_sig_10s.pdf", format="pdf")
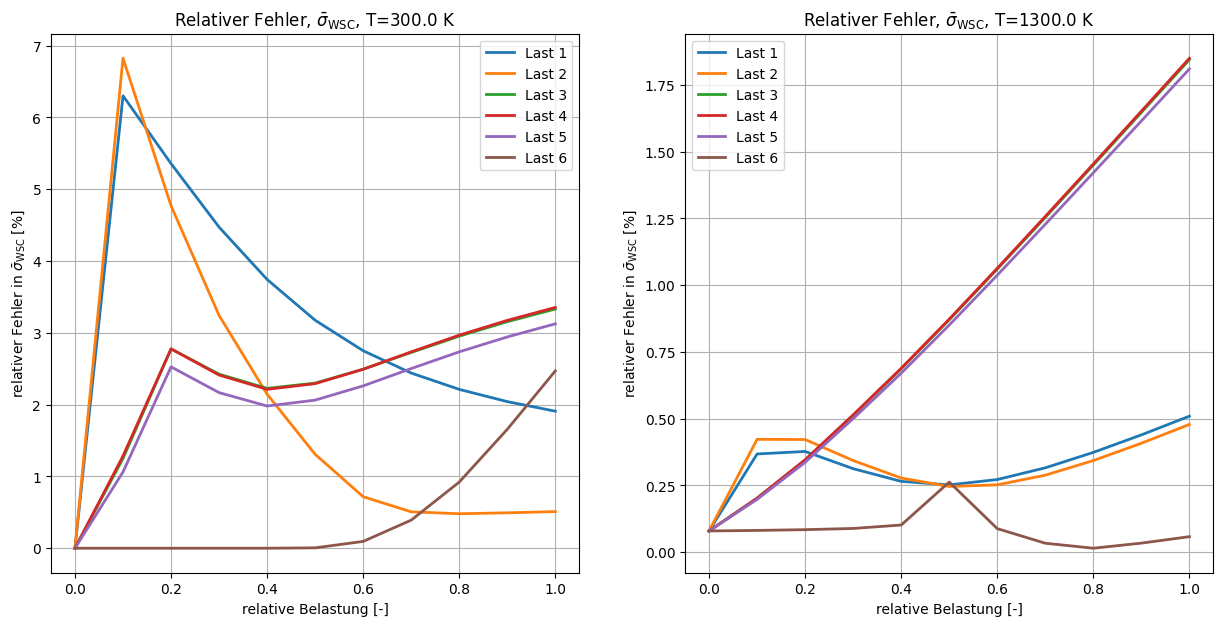
# ### Stress in phase 1 (WSC)
[9]:
fig, axx = plt.subplots(1, 2, figsize=(15, 7))
ct = 0
for i_T, T in zip((0, 9), (300.0, 1300.0)):
ax = axx[ct]
ct += 1
ax.set_title(r"Relativer Fehler, $\bar{\sigma}_{\rm WSC}$, T=%.1f K" % T)
x = np.linspace(0, 1, 11)
ax.set_xlabel("relative Belastung [-]")
ax.set_ylabel(r"relativer Fehler in $\bar{\sigma}_{\sf WSC}$ [%]")
for n in range(6):
myerr = (
np.linalg.norm(fans_S1[i_T][n][:, :] - ntfa_S1[i_T][n][:, :], axis=1)
* 100.0
/ np.linalg.norm(fans_S1[i_T][n][:, :], axis=1)
)
# myerr[0] = 0.
ax.plot(x, myerr, lw=2, label=f"Last {n + 1}")
ax.legend()
ax.grid()
# fig.savefig( f'rel_error_ms9p_T{T:.0f}.pdf', format='pdf', pad_inches=0.0)
plt.savefig("rel_err_sig_wsc_10s.pdf", format="pdf")
Save all results to H5 file
[10]:
F = h5py.File(
os.path.join(data_path, "results", "all_results_ms9p_16x16x16_100s_N24.h5"), "w"
)
F.create_dataset("/eps", data=ntfa_eps)
F.create_group("/ntfa")
F.create_group("/fans")
F.create_dataset("/temperature", data=np.array(temp_list))
F.create_dataset("/fans/sig", data=fans_S)
F.create_dataset("/fans/sig0", data=fans_S0)
F.create_dataset("/fans/sig1", data=fans_S1)
F.create_dataset("/ntfa/sig", data=ntfa_S)
F.create_dataset("/ntfa/sig0", data=ntfa_S0)
F.create_dataset("/ntfa/sig1", data=ntfa_S1)
F.create_dataset("/ntfa/q", data=ntfa_q)
F.create_dataset("/ntfa/xi", data=ntfa_xi)
F.close()
[11]:
# fans_E = np.array(F["ms_9p/dset0_sim/loadcases_0300.00"])[:,20:30]
# fans_S = np.array(F["ms_9p/dset0_sim/hom_response_0300.00"])[:,20:30]
# fans_S0 = np.array(F["ms_9p/dset0_sim/hom_response0_0300.00"])[:,20:30]
# fans_S1 = np.array(F["ms_9p/dset0_sim/hom_response1_0300.00"])[:,20:30]
# F.close()
# fname = "/home/fritzen/calc/dvs/NTFAthermo_paper/ntfa_hull_res.h5"
# F = h5py.File(fname, "r")
# ntfa_E = np.array(F["eps"])
# ntfa_S = np.array(F["sig"])
# ntfa_S0 = np.array(F["sig0"])
# ntfa_S1 = np.array(F["sig1"])
# F.close()
# #%%
# fig, ax = plt.subplots(1,3,figsize=(20,6))
# icomp = 3
# ax[0].plot(fans_E[icomp,:], fans_S[icomp,:], 'x-', color='black')
# ax[0].plot(ntfa_E[icomp,:], ntfa_S[icomp,:], 'o-', color='blue')
# ax[1].plot(fans_E[icomp,:], fans_S0[icomp,:],'x-', color='black')
# ax[1].plot(ntfa_E[icomp,:], ntfa_S0[icomp,:], 'o-', color='blue')
# ax[2].plot(fans_E[icomp,:], fans_S1[icomp,:], 'x-', color='black')
# ax[2].plot(ntfa_E[icomp,:], ntfa_S1[icomp,:], 'o-', color='blue')
# fig, ax = plt.subplots(1,1)
# ax.plot(fans_E[icomp,:3], fans_S[icomp,:3],'x-', color='black')
# ax.plot(ntfa_E[icomp,:20], ntfa_S[icomp,:20], 'o-', color='blue')